Abstract

Neural networks have recently been used to analyze diverse physical systems and to identify the underlying dynamics. While existing methods achieve impressive results, they are limited by their strong demand for training data and their weak generalization abilities to out-of-distribution data. To overcome these limitations, in this work we propose to combine neural implicit representations for appearance modeling with neural ordinary differential equations (ODEs) for modelling physical phenomena to obtain a dynamic scene representation that can be identified directly from visual observations. Our proposed model combines several unique advantages: (i) Contrary to existing approaches that require large training datasets, we are able to identify physical parameters from only a single video. (ii) The use of neural implicit representations enables the processing of high-resolution videos and the synthesis of photo-realistic images. (iii) The embedded neural ODE has a known parametric form that allows for the identification of interpretable physical parameters, and (iv) long-term prediction in state space. (v) Furthermore, the photo-realistic rendering of novel scenes with modified physical parameters becomes possible.

Overview

Our method enables the reconstruction of dynamic scenes based on physical phenomena, such as pendulum motion. We combine neural representations for appearance modeling with explicit dynamics modeling using physical models, resulting in an expressive scene representation constrained by realistic physical motion.

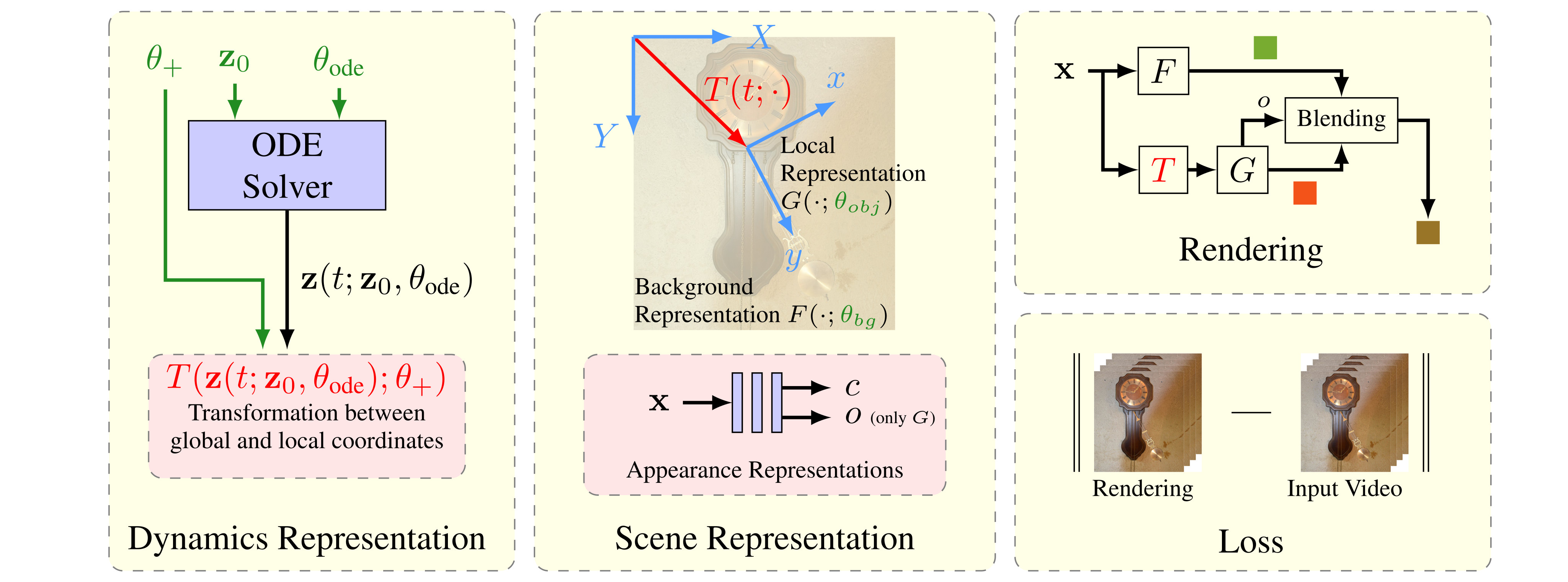
To represent the background and the dynamic object, we use separate MLPs, denoted as $F$ and $G$, which map position to color. We explicitly model the physical phenomenon through the corresponding ODE and use its solution curve to parametrize a transformation $T$ that positions the dynamic object within the scene in a time-dependent manner. An opacity value $o$, predicted by $G$, is used to blend the two color values together. The MLP weights, along with the parameters of the ODE, are learned jointly on a per-scene basis.

Reconstruction of Real-World Scenes

Our method enables realistic reconstruction for phenomena like the pendulum shown above or a thrown ball as shown below (speed x0.3).

Physical Editing

Additionally, the explicit physics model allows for intuitive and realistic physical scene editing, such as increasing the damping of the pendulum damping or adjusting the initial position and velocity of the ball.